Data Structures GATE 2018 Solved Questions

Ques 1:A queue is implemented using a non-circular singly linked list. The queue has a head pointer and a tail pointer, as shown in the figure. Let n denote the number of nodes in the queue. Let enqueue be implemented by inserting a new node at the head, and dequeue be implemented by deletion of a node from the tail.

GATE 2018 Q no 3

Which one of the following is the time complexity of the most time-efficient implementation of enqueue and dequeue, respectively, for this data structure?

(A) θ(1), θ(1)

(B) θ(1), θ(n)

(C) θ(n), θ(1)

(D) θ(n), θ(n)

Ans: (B) θ(1), θ(n)

Solution: New node to be inserted is P

Enqueue(){
    P->Data=Data
    P->Next=Head
    Head=P
}

Time Complexity =O(1) Because only pointer manipulation is involved which takes constant time.

Delete Tail

Dequeue(){
    temp=head
    While(temp->Next->Next!=NULL)
         temp=temp->next
    temp->next=NULL
    tail=temp
}

Time Complexity = Time for Traversing list, free the last node and keep track of Tail pointer =O(n)

Ques 2:The postorder traversal of a binary tree is 8,9,6,7,4,5,2,3,1. The inorder traversal of the same tree is 8,6,9,4,7,2,5,1,3. The height of a tree is the length of the longest path from the root to any leaf. The height of the binary tree above is __.

GATE 2018 Q no 20

Ans: 4

Solution:

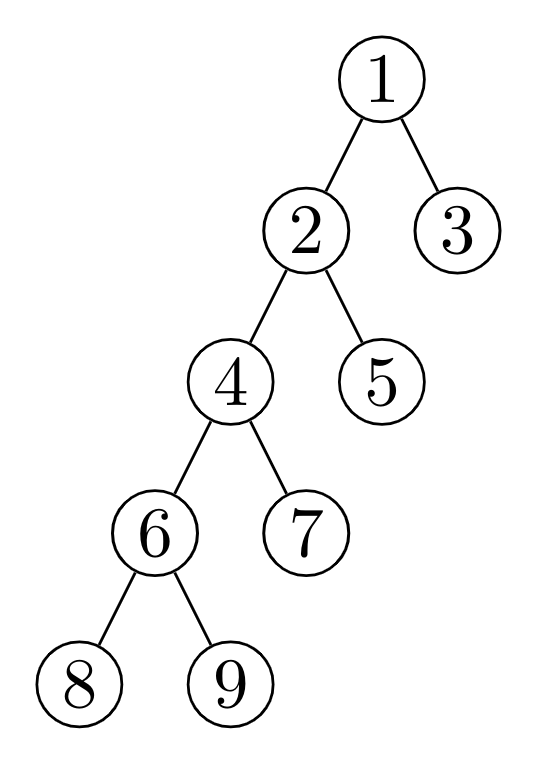
Nodes in longest path from Root to Leaf 

=(1−2,2−4,4−6,6−8) 

or (1−2,2−4,4−6,6−9)

Longest Path|=|(1−2,2−4,4−6,6−8)|=4

Ques 3:Let G be a simple undirected graph. Let T_D be a depth first search tree of G. Let T_B be a breadth first search tree of G. Consider the following statements. (I) No edge of G is a cross edge with respect to T_D. (A cross edge in G is between two
nodes neither of which is an ancestor of the other in T_D.) (II) For every edge (u,v) of G, if u is at depth i and v is at depth j in T_B, then |𝑖 − 𝑗| = 1.

GATE 2018 Q no 30

Which of the statements above must necessarily be true?

(A) I only

(B) II only

(C) Both I and II

(D) Neither I nor II

Ans: (A) I only

Solution: Undirected graph cant have cross edges in DFS forest. (Only directed graphs can have)  ( Hence I is True)

Just draw a triangle SAB. Source is S. Vertex A and B are at same level hence distance 1.  So here |i−j|=0   (Hence II is false)

Ques 4:The number of possible min-heaps containing each value from {1, 2, 3, 4, 5, 6, 7} exactly once is _.

GATE 2018 Q no 46

Ans: 80

Solution: First, let us find probability of getting min heaps from the given elements.

Out of 7 elements, we have to choose minimum element. So probability of getting minimum element from root =1/7

Now for left sub tree we choose 3 elements and out of 3 we have to choose minimum for root of left sub tree.

Probability of getting minimum element for root of left sub tree=1/3

Similarly, probability of getting minimum element for root of right subtree=1/3 

There fore probability of getting a min heap is 1/7*1/3*1/3=1/63.

That is out of 63 structures , 1 structure is a min heap.

Total number of structures possible=7!

There fore out of 7! Structures, 7!/63 = 80 are min heaps.