Ques 1: Which one of the following is a closed form expression for the generating function of the sequence {an}, here an = 2n+3 for all n=0,1,2,…?
GATE 2018 Q No 1
(A) 3/(1−x)2
(B) 3x/(1−x)2
(C) (2−x)/(1−x)2
(D) (3-x)/(1−x)2
Ans: (D) (3-x)/(1−x)2
Solution:

Ques 2: Two people, P and Q, decide to independently roll two identical dice, each with 6 faces, numbered 1 to 6. The person with the lower number wins. In case of a tie, they roll the dice repeatedly until there is no tie. Define a trial as a throw of the dice by P and Q. Assume that all 6 numbers on each dice are equi-probable and that all trials are independent. The probability (rounded to 3 decimal places) that one of them wins on the third trial is ____
GATE 2018 Q no 15
Ans: 0.023
Solution: Here, NOT SUCCESS, p=6/36=1/6
SUCCESS, q=30/36=5/6
So the required case is ppq=p2q
=(1/6)x(1/6) x(5/6)
=5/216
=0.023
Ques 3: The value of ∫ 𝑥 cos(𝑥2)𝑑𝑥 in limits 0 to 𝜋/4 correct to three decimal places (assuming that 𝜋 = 3.14 ) is ___________.
GATE 2018 Q no 16
Ans: 0.27 to 0.30
Solution: Put x2=t
2xdx=dt
t will range from 0 to π2/16
Now our new integral is : ∫ 𝑥 cos(𝑥2)𝑑𝑥 = (1/2)∫cos t dt
= (1/2)[sin(t)]
Putting the limits = (1/2) (sin π2/16 – sin 0)
=(1/2) {sin(.616225)- sin 0}
= (1/2) (0.5779-0)
=0.2889
Ques 4: Consider a matrix A =uvT where
GATE 2018 Q no 17

Note that vT denotes the transpose of v. The largest eigenvalue of A is _.
Ans: 3
Solution:
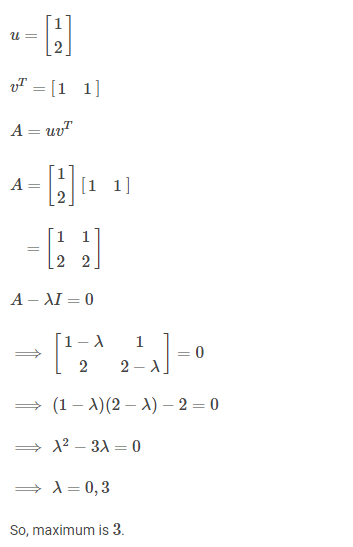
Ques 5: The chromatic number of the following graph is _________
GATE 2018 Q no 18
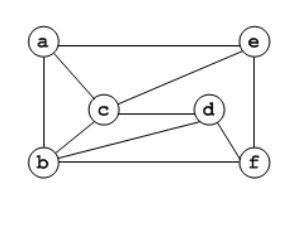
Ans: 3
Solution: The chromatic number of a graph is the smallest number of colors needed to color the vertices of graph so that no two adjacent vertices share the same color.
Here, Independent sets, S1={a,d},S2={b,e},S3={c,f}
Therefore, vertices of S1 has no connection between each other [∵ a & d are not connected by an edge]
S1⇒put COLOR 1
Vertices of S2 has no connection between each other [∵ b & e are not connected by an edge]
S2⇒put COLOR 2
Vertices of S3 has no connection between each other [∵ c & f are not connected by an edge]
S3⇒put COLOR 3
Ques 6: Let G be a finite group on 84 elements. The size of a largest possible proper subgroup of G is __.
GATE 2018 Q no 19
Ans: 42
Solution: Order of a Subgroup always divides the order of Group.
Proper Subgroup of Group having order 84 would have one of the order (proper factors of 84)
2,3,4,6,7,12,14,21,28,42
So the largest order would be 42
Ques 7: Consider a matrix P whose only eigenvectors are the multiples of 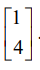
GATE 2018 Q no 26
Consider the following statements.
(I) P does not have an inverse
(II) P has a repeated eigenvalue
(III) P cannot be diagonalized
Which one of the following options is correct?
(A) Only I and III are necessarily true
(B) Only II is necessarily true
(C) Only I and II are necessarily true
(D) Only II and III are necessarily true
Ans: (D) Only II and III are necessarily true
Ques 8: Let N be the set of natural numbers. Consider the following sets.
GATE 2018 Q no 27
P: Set of Rational numbers (positive and negative)
Q: Set of functions from {0, 1} to N
R: Set of functions from N to {0, 1}
S: Set of finite subsets of N.
Which of the sets above are countable?
(A) Q and S only
(B) P and S only
(C) P and R only
(D) P, Q and S only
Ans: (D) P, Q and S only
Solution:
P: Set of Rational numbers are countable. Rational numbers are of the form p/q where p,q are integers.
Q: Set of functions from {0,1} to N. There are N2 such functions. Hence countable.
R: Set of functions from N to {0,1}. There are 2N such functions.
Important theorem If a set S is countable, then P(S) i.e 2S is uncountable.
Hence, statement R is uncountable.
S: Set of finite subsets of N. They are countable.
Important theorem : Every subset of a countable set is either countable or finite.
Hence, Option (D).
Ques 9: Consider the first-order logic sentence
GATE 2018 Q No 28
φ≡∃s∃t∃u∀v∀w∀x∀yψ(s,t,u,v,w,x,y)φ≡∃s∃t∃u∀v∀w∀x∀yψ(s,t,u,v,w,x,y)
where ψ(s,t,u,v,w,x,y) is a quantifier-free first-order logic formula using only predicate symbols, and possibly equality, but no function symbols. Suppose φ has a model with a universe containing 7 elements.
Which one of the following statements is necessarily true?
(A) There exists at least one model of φ with universe of size less than or equal to 3
(B) There exists no model of φ with universe of size less than or equal to 3
(C) There exists no model of φ with universe size of greater than 7
(D) Every model of φ has a universe of size equal to 7
Ans: (A) There exists at least one model of φ with universe of size less than or equal to 3
Ques 10: Let G be a graph with 100! vertices, with each vertex labelled by a distinct permutation of the numbers 1,2, … , 100. There is an edge between vertices 𝑢 and 𝑣 if and only if the label of 𝑢 can be obtained by swapping two adjacent numbers in the label of 𝑣. Let 𝑦 denote the degree of a vertex in G, and 𝑧 denote the number of connected components in G. Then, 𝑦 + 10𝑧 = _.
GATE 2018 Q no 43
Ans: 109
Solution:
We have to find 2 things here, the degree of every vertex(which will be same for all vertices) and number of connected components.
Instead of 100, let’s solve this by taking lesser value, say 4.
With 4! vertices, each vertex is a permutation of {1,2,3,4}.
So, we have vertices like {1,2,3,4}, {1,3,2,4}, {4,1,3,2},… etc.
Here {1,2,3,4} will be connected with
{2,1,3,4}
{1,3,2,4}
{1,2,4,3}
To get this list, just take 2 adjacent numbers and swap them. eg. {1,2,3,4} swap 1 and 2 to get {2,1,3,4}.
The given 3 are the only permutations we can get by swapping only 2 adjacent numbers from {1,2,3,4}.
So, the degree of vertex {1,2,3,4} will be 3. Similarly for any vertex it’s degree will be 3.
Here we got ‘‘3″ because we can chose any 3 pairs of adjacent numbers.
With n vertices, we have n−1 adjacent pairs to swap.
So, degree will be n−1
In our question, degree will be 100−1=99
Now let’s see how many connected components we have.
It will be 1.
If one can reach from one vertex to any other vertex, then that means that the graph is connected.
Now if we start with a vertex say {1,2,3,4} we can reach to other vertex, say {4,3,2,1} by the following path:
{1234}→{1243}→{1423}→{4123}→{4132}→{4312}→{4321}
Just take two adjacent numbers and swap them. With this operation you can create any permutation, from any given initial permutation.
This way you can show that from any given vertex we can reach any other vertex.
This shows that the graph is connected and the number of connected components is 1.
y=99 and z=1
∴y+10z=99+10∗1=109
Ques 11: Consider Guwahati, (G) and Delhi (D)whose temperatures can be classified as high (H), medium (M) and low (L). Let P(HG) denote the probability that Guwahati has high temperature. Similarly, P(MG) and P(LG)denotes the probability of Guwahati having medium and low temperatures respectively. Similarly, we use P(HD),P(MD) and P(LD) for Delhi.
GATE 2018 Q no 44
The following table gives the conditional probabilities for Delhi’s temperature given Guwahati’s temperature.
| HD | MD | LD | |
| HG | 0.40 | 0.48 | 0.12 |
| MG | 0.10 | 0.65 | 0.25 |
| LG | 0.01 | 0.50 | 0.49 |
Consider the first row in the table above. The first entry denotes that if Guwahati has high temperature (HG) then the probability of Delhi also having a high temperature (HD) is 0.40; i.e., P(HD∣HG)=0.40 Similarly, the next two entries are P(MD∣HG)=0.48 and P(LD∣HG)=0.12. Similarly for the other rows.
If it is known that P(HG)=0.2,P(MG)=0.5, and P(LG)=0.3, then the probability (correct to two decimal places) that Guwahati has high temperature given that Delhi has high temperature is ________.
Ans: 0.60
Solution: P(HG/HD)=P(HG HD)/P(HD)=0.2*0.4/(0.2*0.4+)