Graduate Aptitude Test in Engineering

Date: 4th Feb 2018

General Aptitude (GA)

Q.1 – Q.5 Carry ONE mark each.

Q. 6 – Q. 10 Carry TWO marks each.

Q 1. “From where are they bringing their books? ________ bringing _______ books from _____.” The words that best fill the blanks in the above sentence are

(A) Their, they’re, there

(B) They’re, their, there

(D) They’re, there, there

Ans: (B) They’re, their, there

Q 2. “A _________ investigation can sometimes yield new facts, but typically organized ones are more successful.” The word that best fills the blank in the above sentence is

(A) meandering

(B) timely

(D) systematic

Ans: (A) meandering

Q 3. The area of a square is d. What is the area of the circle which has the diagonal of the square as its diameter?

(A) πd

(B) πd²

(D) ½ πd

Ans: (D) ½ πd

Solution:

Q 4. What would be the smallest natural number, which when divided either by 20 or by 42 or by 76 leaves a remainder of 7 in each case?

(A) 3047

(B) 6047

(D) 63847

Ans: (C) 7987

Solution: Let n be the smallest number which is divisible by x,y and z and leaves remainder r in each case.

So, n=LCM(x,y,z) + r

x=20,y=42,z=76 and r=7

Smallest number, n=LCM(20,42,76) + 7

n=7980+7=7987

Q 5. What is the missing number in the following sequence?

2, 12, 60, 240, 720, 1440, _____, 0

(A) 2880

(B) 1440

(D) 0

Ans: (B) 1440

Solution: 2 x 6=12

12 x 5 =60

60 x 4 =240

240 x 3 = 720

720 x 2 = 1440

1440 x 1 = 1440

1440 x 0 = 0

Q 6 – Q 10 carry two marks each.

Q 6. In appreciation of the social improvements completed in a town, a wealthy philanthropist decided to gift Rs 750 to each male senior citizen in the town and Rs 1000 to each female senior citizen. Altogether, there were 300 senior citizens eligible for this gift. However, only 8/9th of the eligible men and 2/3rd of the eligible women claimed the gift. How much money (in Rupees) did the philanthropist give away in total?

(A) 1,50,000

(B) 2,00,000

(D) 1,51,000

Ans: (B) 2, 00 , 000

Solution : Let no. of senior male be x

Let no. of senior female be y

x+y= 300

Q 7. If pqr ≠ 0 and p^−x = 1/ q , q^−y =1/r, r^−z =1/p, what is the value of the product xyz?

-1
1/ pqr
1
Pqr

Ans: (C) 1

Solution: pqr≠0

p^−x = 1/ q

taking log on both sides,

log(p^−x )= log(1/ q) = log 1 – log q = 0-log q = -log q

-x log p = -log q

x=log q /log p

Similarly, y=log r/ log q

and, z=log p / log r

So, xyz=1

Q 8. At a party, 60% of the invited guests are male and 40% are female. If 80% of the invited guests attended the party and if all the invited female guests attended, what would be the ratio of males to females among the attendees in the party?

(A) 2:3

(B) 1:1

(D) 2:1

Ans: (B) 1:1

Solution: Let total males and females be 60x and 40x respectively.

Total number of people = (60x + 40x)

Total number of people who attended : 0.8(60x + 40x) = 80x

Let y males attended. It is given all females attended

40x + y = 80x

y = 40x

which is same as females.

Q 9. In the figure below, ∠DEC + ∠BFC is equal to ____________ .

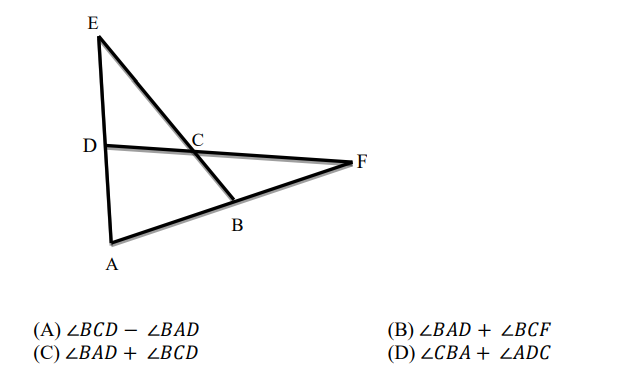
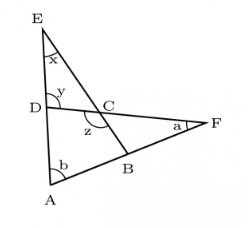
Here, ∠z=∠x+∠y

This is a triangle property that tells us that “the exterior angle of a triangle is the sum of the two opposite interior angle.”

Similarly, ∠y=∠a+∠b

By substituting, we get, ∠Z=∠x+∠a+∠b

Now ∠Z=∠BCD

∠b=∠BAD

Now, ∠BCD−∠BAD

=∠Z−∠b

=∠x+∠a+∠b−∠b

=∠x+∠a

=∠DEC+∠BFC

Q 10. A six sided unbiased die with four green faces and two red faces is rolled seven times. Which of the following combinations is the most likely outcome of the experiment?

(A) Three green faces and four red faces.

(B) Four green faces and three red faces.

(D) Six green faces and one red face.

Ans: (C) Five green faces and two red faces.

Solution: We can calculate the probability of each of the options but by logic or common sense, we can easily eliminate the ones with more number of red faces – option A can be avoided without any calculation.

(A) P(3G,4R) Rejected

(B)P(4G,3R) = ⁷C₄ (⁴/₆)⁴ (²/₆)³