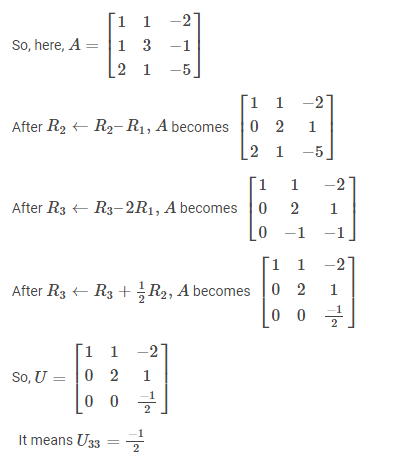Ques 1: Consider the following two statements with respect to the matrices Amxn, Bnxm,Cnxn and Dnxn
GATE 2022 Q No 20
Statement 1: tr(AB) = tr(BA)
Statement 2: tr(CD) = tr(DC)
where tr() represents the trace of a matrix. Which one of the following holds?
(A) Statement 1 is correct and Statement 2 is wrong.
(B) Statement 1 is wrong and Statement 2 is correct.
(C) Both Statement 1 and Statement 2 are correct.
(D) Both Statement 1 and Statement 2 are wrong.
Ans: (C) Both Statement 1 and Statement 2 are correct.
Solution: Trace of a matrix and sum of eigen values of matrix are same.
AB and BA has same nonzero eigen values hence their sum of eigen values i.e. trace should also be same.
Statement 2 follows from statement 1 since both are square matrices.
So both statements are correct.
Ques 2: Which of the following statements is/are TRUE for a group G?
GATE 2022 Q No 27
(A) If for all x,y∈G, (xy)2=x2y2, then G is commutative.
(B) If for all x∈G, x2=1 then G is commutative. Here, 1 is the identity element of G.
(C) If the order of G is 2, then G is commutative.
(D) If G is commutative, then a subgroup of G need not be commutative.
Ans: (A) , (B) , (C)
Solution: (A) If for all x,y∈G, (xy)2=x2y2, then G is commutative. True
Since (ab)(ab)=(aa)(bb)
We know that in a group, left and right cancellation is allowed.
So, Cancel left most “a” on both sides and Cancel right most “b” on both sides.
We get ba=ab.
(B) If for all x∈G, x2=1 then G is commutative. Here, 1 is the identity element of G. True
Let a,b be two elements in group G.
It is given that (ab)2=1
(ab)(ab)=1,
So ab is inverse of ab
Now consider (ab)(ba)
(ab)(ba)=a(bb)a=aa=1
So, (ab)(ba)=1 which means that ba is inverse of ab.
But every element in a group has unique inverse, So, ab=ba
Hence, G is abelian.
(C) If the order of G is 2, then G is commutative. True
Every group of order less than or equal to five is abelian.
(D) If G is commutative, then a subgroup of G need not be commutative. False
In Abstract Algebra, “Abelian” word is used as a synonym of “commutative”. and acc. to theorem
Every subgroup of an abelian group has to be abelian.
Ques 3: The number of arrangements of six identical balls in three identical bins is______
GATE 2022 Q No 32
Ans: 7
Solution:
Case 1 : If only one bin is used : (6,0,0) i.e. Only 1 way (Since All balls have to be put in this single bin that is used and Since all bins are identical, so, it doesn’t matter which bin we use)
Case 2 : If two bins are used
The distribution can be done as any of the following :
(5,1,0) (which means 5 identical balls in one bin, 1 ball in another bin, and the third bin is unused)
(4,2,0) (which means 4 identical balls in one bin, 2 balls in another bin, and the third bin is unused)
(3,3,0) (which means 3 identical balls in one bin, 3 balls in another bin, and the third bin is unused) i.e. 3 ways to distribute 6 identical balls into 3 identical bins if exactly two of the bins are used.
Case 3 : If three bins are used:
The distribution can be done as any of the following :
(4,1,1) (which means 4 identical balls in one bin, 1 ball in another bin, and 1 ball in the third bin)
(3,2,1) (which means 3 identical balls in one bin, 2 ball in another bin, and 1 ball in the third bin)
(2,2,2) (which means 2 identical balls in one bin, 2 ball in another bin, and 2 ball in the third bin) i.e. 3 ways to distribute 6 identical balls into 3 identical bins if all three of the bins are used.
So, total we have 1 + 3 + 3 = 7 ways to distribute 6 identical balls in 3 identical bins.
Ques 4: The value of the following limit is ________________.
GATE 2022 Q No 34
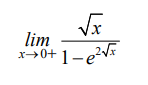
Ans: -0.5
Solution: Apply L Hospital Rule
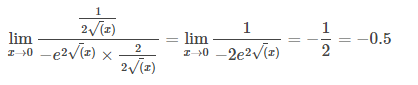
Ques 5: Which one of the following is the closed form for the generating function of the sequence {an} n≥0 defined below?
GATE 2022 Q No 36
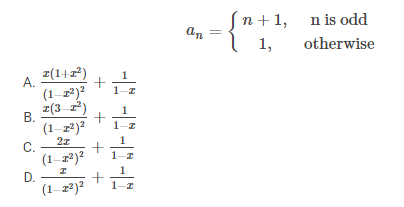
Ans: (A)
Solution: Corresponding Sequence would be –
a0, a1, a2, a3, a4, …∞
=1, 2, 1, 4, 1, 6, 1, 8, 1, 10, 1…∞
=1×0+ 2×1 + 1×2 + 4×3 + 1×4 + 6×5 + 1×6 + 8×7 + 1×8 + 10×9 + 1×10…
= (1x0+1x2+1x4+…∞) + (2x1 + 4x3 + 6x5 + 8x7 + 10x9 + …∞)
= A + B
A = 1 + x2 + x4 + x6 + …∞
= Sum of GP Series where a = 1 and r= x2
= a / (1-r)
=1/(1−x2)
B = 2x1 + 4x3 + 6x5 + 8x7 + 10x9 + …∞
= Sum of AP and GP. (Where 2,4,6,8,10 forms a AP and x1,x3,x5,x7,x9 forms a GP
x2B = 2x3 + 4x5 + 6x7 + 8x9 + 10x11 + …∞
B – x2B = (2x1 + 4x3 + 6x5 + 8x7 + 10x9 + …∞) – ( 2x3 + 4x5 + 6x7 + 8x9 + 10x11 + …∞)
(1-x2)B = 2x1 + 2x3 + 2x5 + 2x7 + 2x9 + …∞
(1-x2)B = 2x (1 + x2 + x4 + x6 + …∞)
(1-x2)B = 2x / (1-x2)
B = 2x / (1-x2)2

Ques 6: Consider a simple undirected unweighted graph with at least three vertices. If A is the adjacency matrix of the graph, then the number of 3–cycles in the graph is given by the trace of
GATE 2022 Q No 37
(A) A3
(B) A3 divided by 2
(C) A3 divided by 3
(D) A3 divided by 6
Ans: (D) A3 divided by 6
Solution: Take a cycle graph on 3 vertices i.e. C3.
Write the adjacency matrix A of C3, find A3.
The trace of A3 is 6, but we only have one 3-cycle(3 length cycle) in C3.
So, we have to divide the trace of A3 by 6 to find out the number of 3-cycles.
Ques 7: Consider solving the following system of simultaneous equations using LU decomposition.
GATE 2022 Q No 45
x1 + x2 – 2x3 = 4
x1 + 3x2 – x3 = 7
2x1 + x2 – 5x3 = 7
where L and U are denoted as
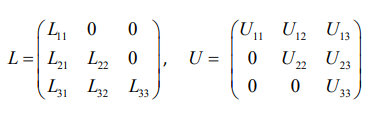
Which one of the following is the correct combination of values for L32 , U33 , and x1 ?
(A) L32=2, U33=–1/2, x1=–1
(B) L32=2, U33=2, x1=–1
(C) L32=–1/2, U33=2, x1=0
(D) L32=–1/2, U33=–1/2, x1=0
Ans: (D) L32=–1/2, U33=–1/2, x1=0
Solution:
- x1 + x2 – 2x3 = 4 eq(1)
- x1 + 3x2 – x3 = 7 eq(2)
- 2x1 + x2 – 5x3 = 7 eq(3)
2eq(2)–eq(3) gives 5x2+3x3=7
2eq(1)–eq(3) gives x2+x3=1 ⟹5x2+5x3=5
solving these two equations, x3 = -1 , x2 = 2
Putting these values in equation 1, we get x1 = 0
To find LU decomposition (if it is possible), we only need to convert the given matrix into U by elementary row operations in Gaussian elimination method.