Ques 1: A problem in NP is NP-complete if
GATE 2006
(A) it can be reduced to the 3-SAT problem in polynomial time
(B) the 3-SAT problem can be reduced to it in polynomial time
(C) it can be reduced to any other problem in NP in polynomial time
(D) some problem in NP can be reduced to it in polynomial time
Ans: (A) it can be reduced to the 3-SAT problem in polynomial time
Solution: 3-SAT is NPC
So, reducing a NP problem to 3-SAT means NP problem is NPC
Ques 2: For problems X and Y, Y is NP-complete and X reduces to Y in polynomial time. Which of the following is TRUE?
GATE 2008
(A) If X can be solved in polynomial time, then so can Y
(B) X is NP-complete
(C) X is NP-hard
(D) X is in NP, but not necessarily NP-complete
Ans: (B) X is NP-complete
Solution: X is reducible to NPC.
So, X is also NPC
Ques 3: Let πA be a problem that belongs to the class NP. Then which one of the following is TRUE?
GATE 2009
(A) There is no polynomial time algorithm for πA
(B) If πA can be solved deterministically in polynomial time, then P = NP.
(C) If πA is NP-hard, then it is NP-complete.
(D) πA may be undecidable.
Ans: (C) If πA is NP-hard, then it is NP-complete.
Solution: If πA is NP hard, and belongs to NP means it is NP Complete
Ques 4: Which of the following statements are TRUE?
GATE 2013
- The problem of determining whether there exists a cycle in an undirected graph is in P
- The problem of determining whether there exists a cycle in an undirected graph is in NP.
- If a problem A is NP−Complete, there exists a non-deterministic polynomial time algorithm to solve A
(A) 1, 2 and 3
(B) 1 & 3 only
(C) 2 only
(D) 3 only
Ans: (A) 1, 2 and 3
Solution: Using DFS, we can find whether there exists a cycle in an undirected graph in O(n2) time.
So it is P problem
Since P is a subset of NP, is is also NP problem
option 3 is also true being the definition of NP-Complete
So all are True
Ques 5: Suppose a polynomial time algorithm is discovered that correctly computes the largest clique in a given graph. In this scenario, which one of the following represents the correct Venn diagram of the complexity classes P, NP and NP Complete (NPC)?
GATE 2014 Set 1
(A) 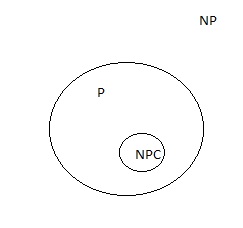
(B) 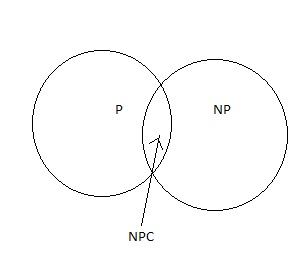
(C) 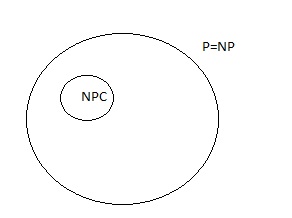
(D) 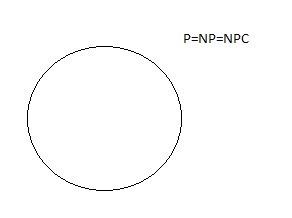
Ans: (D)
Solution: Clique is NP-Complete Problem.
If Clique is P, then P=NPC
So, P=NP=NPC