Algorithm GATE 2018 Solved Questions

Ques 1:Assume that multiplying a matrix G1 of dimension 𝑝 × 𝑞 with another matrix G2 of dimension 𝑞 × 𝑟 requires 𝑝𝑞𝑟 scalar multiplications. Computing the product of n matrices G₁G₂G₃…G_n can be done by parenthesizing in different ways. Define G_i G_i+1 as an explicitly computed pair for a given paranthesization if they are directly multiplied. For example, in the matrix multiplication chain G₁G₂G₃G₄G₅G₆ using parenthesization (G₁(G₂G₃))(G₄(G₅G₆)), G₂G₃ and G₅G₆ are the only explicitly computed pairs. Consider a matrix multiplication chain F₁F₂F₃F₄F₅, where matrices F₁, F₂, F₃, F₄ and F₅ are of dimensions 2×25, 25×3, 3×16, 16×1 and 1×1000, respectively. In the parenthesization of F₁F₂F₃F₄F₅ that minimizes the total number of scalar multiplications, the explicitly computed pairs is/are

GATE 2018 Q no 31

(A) F₁F₂ and F₃F₄ only

(B) F₂F₃ only

(C) F₃F₄ only

(D) F₁F₂ and F₄F₅ only

Ans: (C) F₃F₄ only

Solution: If we multiply anything with F₅ we will get much greater multiplication cost because F₅ is 1∗1000 matrix so 1000 will play vital role in cost. So we will multiply F₅ at very last step.

So, here is the sequence giving minimal cost:

(F₁(F₂(F₃F₄)))(F₅)=48+75+50+2000=2173

Explicitly computed pairs is F₃F₄

Ques 2:Consider the following undirected graph G

GATE 2018 Q no 47

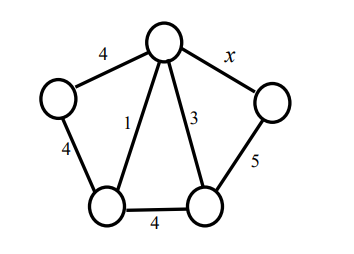
Choose a value for x that will maximize the number of minimum weight spanning trees (MWSTs) of G. The number of MWSTs of G for this value of x is __.

Ans: 4

Solution: We can use Kruskal algo. i.e. keep selecting min weight edges and if a cycle occurs then ignore that edge.

Do this until you select n−1 edges.

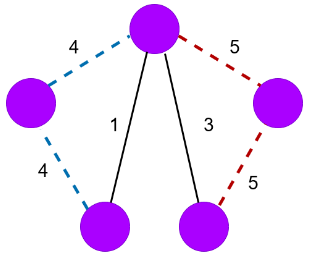
Total= 2x 2 = 4 choices

Ques 3: Consider the weights and values of items listed below. Note that there is only one unit of each item.

GATE 2018 Q no 48

Item number (in Kgs)	Weight	Value (in Rupees)
1	10	60
2	7	28
3	4	20
4	2	24

The task is to pick a subset of these items such that their total weight is no more than 11 Kgs and their total value is maximized. Moreover, no item may be split. The total value of items picked by an optimal algorithm is denoted by 𝑉_opt. A greedy algorithm sorts the items by their value-to-weight ratios in descending order and packs them greedily, starting from the first item in the ordered list. The total value of items picked by the greedy algorithm is denoted by 𝑉_greedy.

The value of 𝑉_opt − 𝑉_greedy is __.

Ans: 16

Solution: V_opt is clearly 60.

You can go for brute force or by normal intuition you can get it.

Now solving for V_greedy

Item number (in Kgs)	Weight	Value (in Rupees)	Value/Weight
1	10	60	6
2	7	28	4
3	4	20	5
4	2	24	12

Sort them in descending order of Value/Weight as per the question.

Item number (in Kgs)	Weight	Value (in Rupees)	Value/Weight
4	2	24	12
1	10	60	6
3	4	20	5
2	7	28	4

• Item 4 is picked. Weight remaining = 11−2=9
• Item 1 cannot be picked as 10kg >9kg.
• Item 3 can be picked as 4kg < 9kg. Weight Remaining = 9−4=5kg
• Item 2 cannot be picked as 7kg >5kg.

So, item 4 and Item 3 are picked. Their values are 24 and 20 respectively.

V_greedy=24+20=44.

V_optimal−V_greedy=60−44=16.