Algorithm GATE 2022 Solved Questions

Ques 1:Which one of the following statements is TRUE for all positive functions f(n)?

GATE 2022 Q no 11

(A) f(n²)=θ(f(n)²), when f(n) is a polynomial

(B) f(n²)=o(f(n)²)

(C) f(n²)=O(f(n)²), when f(n) is an exponential function

(D) f(n²)=Ω(f(n)²)

Ans: (A) f(n²)=θ(f(n)²), when f(n) is a polynomial

Solution: Analyse, f(n²) versus f(n)² asymptomatically

• Take f(n)=log n
• f(n²)= log n² = 2 log n 
• f(n)²=(log n)²
• Here f(n²)<f(n)²

• Take f(n)=eⁿ  
• f(n²)=eⁿ²
• f(n)²=eⁿeⁿ=e²ⁿ.
• Here f(n²)>f(n)² because n²>2n

• Take f(n) as polynomial say, f(n)=n³ 
• f(n²)=n⁶
• f(n)²=n⁶.
• Here  f(n²)=f(n)²

Ques 2: Consider a simple undirected weighted graph G, all of whose edge weights are distinct. Which of the following statements about the minimum spanning trees of G is/are TRUE?

GATE 2022 Q no 49

(A) The edge with the second smallest weight is always part of any minimum spanning tree of G.

(B) One or both of the edges with the third smallest and the fourth smallest weights are part of any minimum spanning tree of G.

(C) Suppose S⊆V be such that S≠ϕ and S≠V. Consider the edge with the minimum weight such that one of its vertices is in S and the other in V/S. Such an edge will always be part of any minimum spanning tree of G.

(D) G can have multiple minimum spanning trees.

Ans:

Answer : (A) , (B) , (C)

In the given undirected weighted graph, All the edge weights are distinct, hence, there will be Exactly One Minimum Spanning Tree for the graph.

Option A : The edge with the second smallest weight is always part of any minimum spanning tree of G. True

Minimum Edge, Second Minimum Edge, both will always be added in the MST by Kruskal Algorithm (Because Two edges cannot bring cycle)

Option B :One or both of the edges with the third smallest and the fourth smallest weights are part of any minimum spanning tree of G. True

Minimum Edge, Second Minimum Edge, both will be added in the MST by Kruskal Algorithm (Two edges cannot bring cycle), BUT third minimum edge might introduce cycle in the MST, and if so happens, we do not include third minimum edge in the MST and add fourth minimum edge in the MST.

Option C : Suppose S⊆V be such that S≠ϕ and S≠V . Consider the edge with the minimum weight such that one of its vertices is in S and the other in V−S . Such an edge will always be part of any minimum spanning tree of G. True.

This is a popular and basic property of Minimum Spanning Tree, known as “Cut Property.” 

Option D : G can have multiple minimum spanning trees : False (Because all edge weights are distinct)

Ques 3: Let G( V, E) be a directed graph, where V {1, 2,3, 4, 5} is the set of vertices and E is the set of directed edges, as defined by the following adjacency matrix A

GATE 2022 Q no 58

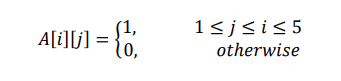
𝐴[𝑖][𝑗] = 1 indicates a directed edge from node i to node j. A directed spanning tree of G, rooted at r belongs to V , is defined as a subgraph T of G such that the undirected version of T is a tree, and T contains a directed path from r to every other vertex in V. The number of such directed spanning trees rooted at vertex 5 is_____________

Ans: 24

Solution: Directed Spanning Tree(DST) is basically a Directed Acyclic Graph(DAG) whose root node is 5, and it contains all the vertices.

We need to find how many such DAGs are possible

5 is the root node of the DAG. Let’s fix this at one place and permute all other numbers.

Total there are 4!=24 permutations possible.