Ques 1:Consider the problem of reversing a singly linked list. To take an example, given the linked list below,
GATE 2022 Q no 15

the reversed linked list should look like

Which one of the following statements is TRUE about the time complexity of algorithms that solve the above problem in O(1) space?
(A) The best algorithm for the problem takes θ(n) time in the worst case.
(B) The best algorithm for the problem takes θ(n log n) time in the worst case.
(C) The best algorithm for the problem takes θ(n2) time in the worst case.
(D) It is not possible to reverse a singly linked list in O(1) space.
Ans: (A) The best algorithm for the problem takes θ(n) time in the worst case.
Solution: Reversing a linked list only requires one traversal of entire linked list of N elements and Change the appropriate Pointers.
Algorithm:
- struct node * reverse( struct node * head )
- {
- struct node * prevP = NULL;
- struct node * nextP = head->next;
- while(head != NULL)
- {
- head->next = prevP;
- prevP = head;
- head = nextP;
- nextP = head->next;
- }
- return prevP;
- }
Time complexity – θ(n)
Space Complexity – O(1)
Ques 2: Suppose we are given n keys, m hash table slots, and two simple uniform hash functions h1 and h2 . Further suppose our hashing scheme uses h1 for the odd keys and h2 for the even keys. What is the expected number of keys in a slot?
GATE 2022 Q no 16
(A) m/n
(B) n/m
(C) 2n/m
(D) n/2m
Ans: (B) n/m
Solution: We can find this using probability.
Let X = Number of items in slot 1. (Note that I am only talking about some random slot, say slot 1 )
Xi={1, if i th item maps to slot and 0, otherwise }
X=X1+X2+…Xn
E[X]=E[X1+X2+…Xn]
E[X]=E[X1]+E[X2]+…E[Xn]
Now, calculate E[Xi]
P(Xi=1)=1/m because whatever happens within black box ( h1 or h2), the overall hash function will be uniform.
E[Xi]=1P(Xi=1)+0P(Xi=0)=1/m
Hence, E[X]=n/m
Ques 3: Suppose a binary search tree with 1000 distinct elements is also a complete binary tree. The tree is stored using the array representation of binary heap trees. Assuming that the array indices start with 0, the 3rd largest element of the tree is stored at index_____________.
GATE 2022 Q no 28
Ans: 509
Solution: For 1000 elements, there will be 10 levels (root is at level 1).
But last level will not be completely filled since there are only 1000 elements, and we need 1023 nodes to fill all levels.
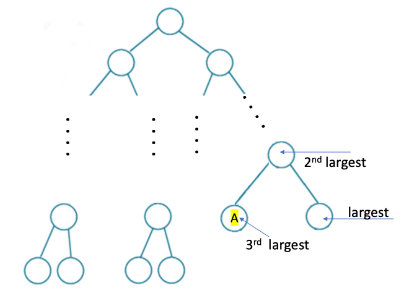
Now, largest will be at rightmost of 9th level.
And, 2nd largest will at rightmost of 8th level.
Since we know that in-order traversal of BST is sorted hence 3rd largest will be a element just before 2nd largest in in-order.
Now, index of 2nd largest. (Assuming index starts from 1)
1→3→7→15→31→63→127→255
Index of 3rd largest = 510
Since indices are starting from 0 hence answer is 509
Ques 4: Consider a simple undirected graph of 10 vertices. If the graph is disconnected, then the maximum number of edges it can have is _______________ .
GATE 2022 Q no 30
Ans: 36
Solution: To get maximum number of edges we can isolate 1 vertex and make a complete graph of 9 vertices.
Max. number of edges with 9 vertices = (9×8) /2 = 72/2 = 36
Ques 5: Consider the queues Q1 containing four elements and Q2 containing none (shown as the Initial State in the figure). The only operations allowed on these two queues are Enqueue(Q,element) and Dequeue(Q). The minimum number of Enqueue operations on Q1 required to place the elements of Q1 in Q2 in reverse order (shown as the Final State in the figure) without using any additional storage is___________.
GATE 2022 Q no 62
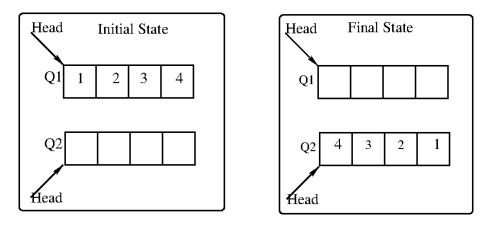
Ans:
Step 0: Enqueue 1 in Q2.
Step 1: Enqueue 2 in Q2 i.e 1,2
Step 2: perform 1 dequeue and 1 enqueue simultaneously for 1 time in Q2 i.e 2,1
Step 3: enqueue 3 in Q2 i.e 2,1,3
Step 4: perform 1 dequeue and 1 enqueues in simultaneously for 2 times in Q2 i.e 2,1,3 → 1,3,2 → 3,2,1
Step 5: Enqueue 4 in Q2 i.e 3,2,1,4
Step 6: perform 1 dequeue and 1 enqueues in simultaneously for 3 times in Q2 i.e 3,2,1,4 → 2,1,4,3 → 1,4,3,2 → 4,3,2,1
So the number of enqueue operations in Q1 is 0.