Ques 1:In a relational data model, which one of the following statements is TRUE?
GATE 2022 Q no 14
(A) A relation with only two attributes is always in BCNF.
(B) If all attributes of a relation are prime attributes, then the relation is in BCNF.
(C) Every relation has at least one non-prime attribute
(D) BCNF decompositions preserve functional dependencies
Ans: (A) A relation with only two attributes is always in BCNF.
Solution:
(A) It is true to say that every binary relation is always in BCNF
(B) This is false because it is not necessary to have a relation in BCNF if all the attributes are prime attributes.
For example, R(A, B, C) with FD A -> C, B -> C, C -> A
Here all the attributes are prime but it is not in BCNF.
(C) No, it is not necessary to have at least one non-prime attribute in a relation
(D) No, it is not necessary that every lossless BCNF decomposition is dependency preserving
Ques 2: Consider the following three relations in a relational database.
GATE 2022 Q no 25
Employee (eId ,Name), Brand (bId ,bName), Own (eId, bId)
Which of the following relational algebra expressions return the set of eIds who own all the brands?
(A) ΠeId(ΠeId,bId(Own)/ΠbId(Brand))
(B) ΠeId(Own)–ΠeId((ΠeId(Own)×ΠbId(Brand))–ΠeId,bId(Own))
(C) ΠeId(ΠeId,bId(Own)/ΠbId(Own))
(D) ΠeId((ΠeId(Own)×ΠbId(Own))/ΠbId(Brand))
Ans: (A) , (B)
Solution: Result is of Division Operator
(A) ΠeId,bId(Own)/ΠbId(Brand) Results eid’s which owns every brand of brand relation.
(B) It is simple expansion and division using basic operators.
Ques 3: Consider a relation R (A, B, C, D, E) with the following three functional dependencies.
GATE 2022 Q no 31
AB → C; BC → D; C → E
The number of super keys in the relation R is ________
Ans: 8
Solution: Here, (AB)+=ABCDE
So, A and B are Independent attributes.
So, Every key must contain A and B.
Remaining Fields are C, D, E
Every attribute has two choices (either add to candidate key or left it), and there are 3 such attributes.
So, No. of super keys = 2x2x2 = 8
Note that Every candidate Key is also Super Key.
Ques 4: Let Ri(z) and Wi(z) denote read and write operations on a data element z by a transaction Ti, respectively. Consider the schedule S with four transactions.
GATE 2022 Q no 39
S:R4(x)R2(x)R3(x)R1(y)W1(y)W2(x)W3(y)R4(y)
Which one of the following serial schedules is conflict equivalent to S?
(A) T1→T3→T4→T2
(B) T1→T4→T3→T2
(C) T4→T1→T3→T2
(D) T3→T1→T4→T2
Ans: (A) T1→T3→T4→T2
Solution: Tabular representation of given schedule is :
| Line | T1 | T2 | T3 | T4 |
| 1 | R(X) | |||
| 2 | R(X) | |||
| 3 | R(X) | |||
| 4 | R(y) | |||
| 5 | W(y) | |||
| 6 | W(x) | |||
| 7 | W(y) | |||
| 8 | W(y) |
- Line 1 and Line 6 are conflict operations. So in Serial schedule Transaction T4 must be before T2
- Line 3 and Line 6 are conflict operations. So in Serial schedule Transaction T3 must be before T2
- Line 4 and Line 7 are conflict operations. So in Serial schedule Transaction T1 must be before T3
- Line 5 and Line 8 are conflict operations. So in Serial schedule Transaction T1 must be before T4
- Line 7 and Line 8 are conflict operations. So in Serial schedule Transaction T3 must be before T4
Accumulating all these points, T1 should be first followed by T3 , T4 and T2 in order.
Ques 5: Consider the relational database with the following four schemas and their respective instances.
GATE 2022 Q no 56
Student(sNo, sName, dNo) Dept(dNo, dName) Course(cNo, cName, dNo) Register(sNo, cNo)
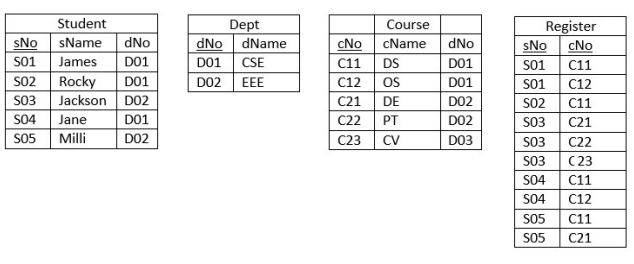
SQL Query:
SELECT * FROM Student AS S WHERE NOT EXIST (SELECT cNo FROM Course WHERE dNo = “D01” EXCEPT SELECT cNo FROM Register WHERE sNo = S.sNo)
The number of rows returned by the above SQL query is___________.
Ans: 2
Solution: Query returns the tuples from S where students who’re registered with all the courses which are associated with D01 department.
By seeing the relation instances, we can understand that only two students from S ( S01 and S04) , registered with all the courses which are associated with D01 department.