Ques 6: The simultaneous equations on the Boolean variables x,y,z and w
GATE 2000
x+y+z=1
xy=0
xz+w=1
xy+z’w’=0
have the following solution for x,y,z and w, respectively:
(A) 0 1 0 0
(B) 1 1 0 1
(C) 1 0 1 1
(D) 1 0 0 0
Ans : C) 1 0 1 1
Solution: x + y + z = 1 means anyone of x ,y , z can be 1
xy=0 means either x=0 or both x=y=0. So (B)cant be True
xz+w=1 means either x,z both 1 or w is 1. So (A) and (D) cant be true
So ( C) Is True
Ques 7: Which functions does NOT implement the Karnaugh map given below?
GATE 2000
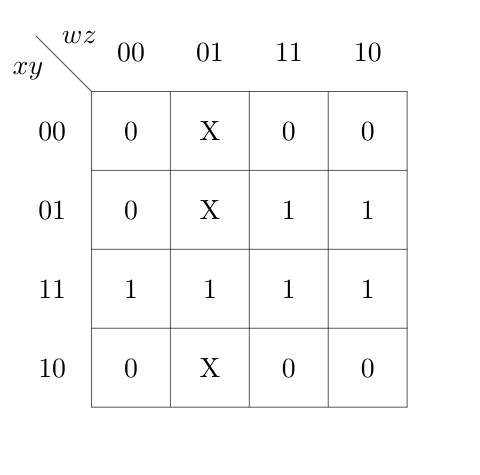
(A) (w+x)y
(B) xy+yw
(C) (w+x)(w+y)(x+y)
(D) None of the above
Ans: (C) (w+x)(w+y)(x+y)
Solution: K-Map is
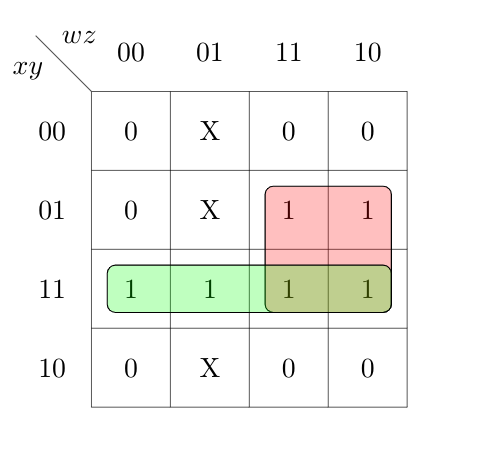
xy + wy
Option A & B represent same expression
Ques 8: Given the following karnaugh map, which one of the following represents the minimal Sum-Of-Products of the map?
GATE 2001
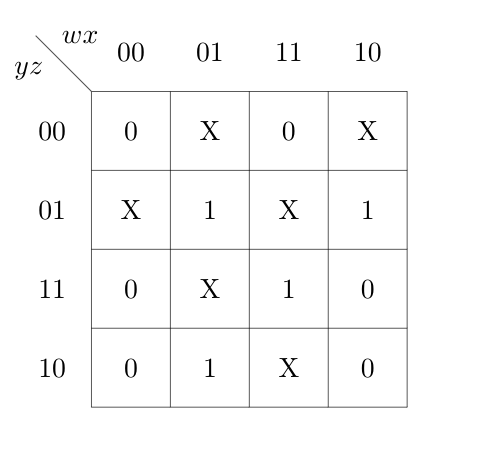
(A) xy + y’z
(B) wx’y’ + xy + xz
(C) w’x + y’z + xy
(D) xz + y
Ans: (A) xy + y’z
Solution:
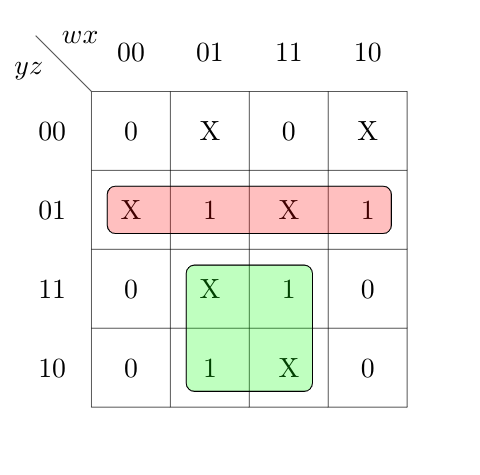
Ques 9: Minimum sum of product expression for f(w,x,y,z)f(w,x,y,z) shown in Karnaugh-map below
GATE 2002
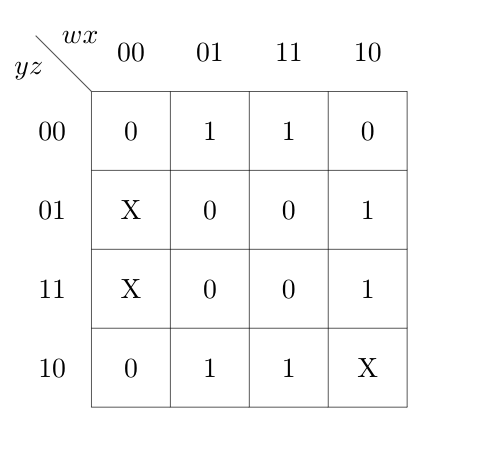
(A) xz + y’z
(B) xz’ + zx’
(C) x’y + zx’
(D) None of these
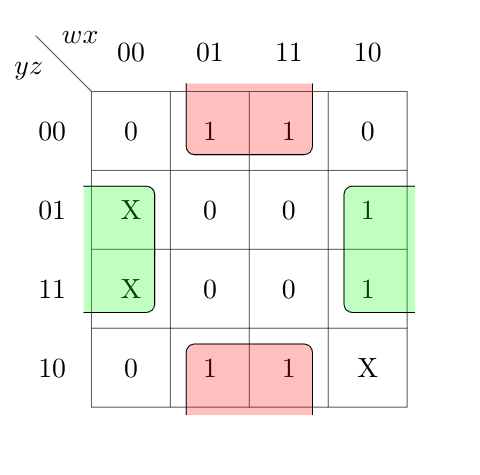
Ans: B) xz’ + zx’
Solution:
Ques 10: Consider the following logic circuit whose inputs are functions f1,f2,f3 and output is f
GATE 2002
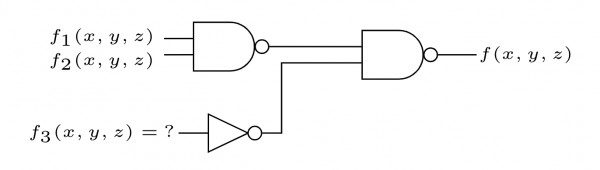
Given that
f1(x,y,z)=Σ(0,1,3,5)
f2(x,y,z)=Σ(6,7) and
f(x,y,z)=Σ(1,4,5).
f3 is
(A) Σ(1,4,5)
(B) Σ(6,7)
(C) Σ(0,1,3,5)
(D) None of these
Ans: (A) Σ(1,4,5)
Solution: f=((f1f2)′f3′)′=f1f2+f3
f1f2=0 (as no common term in both)
So f=f3=Σ(1,4,5)