Ques 11: Let f(A,B)=A′+B Simplified expression for function f(f(x+y,y),z) is
GATE 2002
(A) x’ + z
(B) xyz
(C) xy’ + z
(D) none of these
Ans: C) xy’ + z
Solution: f(f(x+y,y),z)
=f((x+y)’+ y ,z)
=f(x’y’ + y , z)
=f(x’+y , z)
=(x’ + y) ‘ + z
=xy’ + z
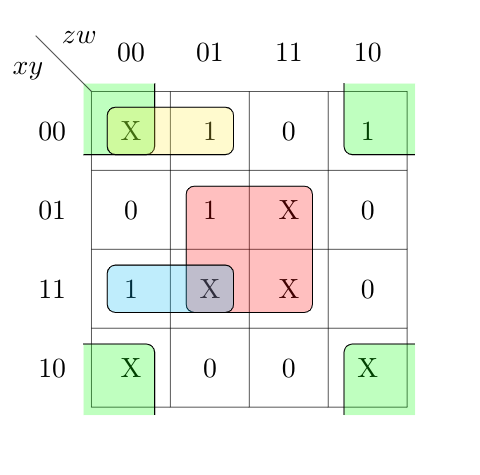
Ques 12: The literal count of a Boolean expression is the sum of the number of times each literal appears in the expression. For example, the literal count of (xy+xz′) is 4. What are the minimum possible literal counts of the product-of-sum and sum-of-product representations respectively of the function given by the following Karnaugh map? Here, X denotes “don’t care”
GATE 2003

(A) 11,9
(B) 9,13
(C) 9,10
(D) 11,11
Ans: (C) 9,10
Solution: POS=3+2+2+2=9
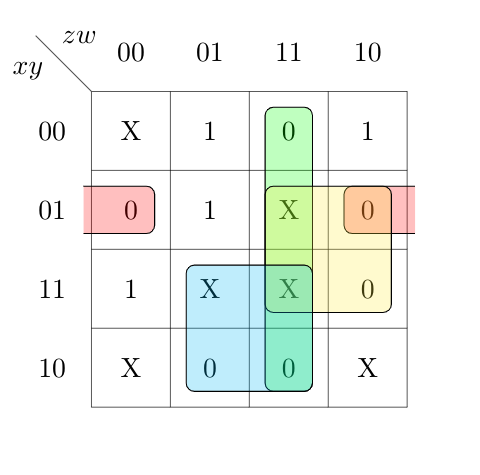
SOP=2+2+3+3=10
Ques 13: Consider the following circuit composed of XOR gates and non-inverting buffers.
GATE 2003
The non-inverting buffers have delays δ1=2ns and δ2=4ns as shown in the figure. Both XOR gates and all wires have zero delays. Assume that all gate inputs, outputs, and wires are stable at logic level 0 at time 0. If the following waveform is applied at input A, how many transition(s) (change of logic levels) occur(s) at B during the interval from 0 to 10 ns?

(A) 1
(B) 2
(C) 3
(D) 4
Ans: (D) 4
Solution:
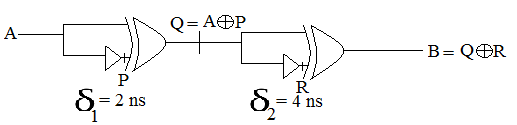
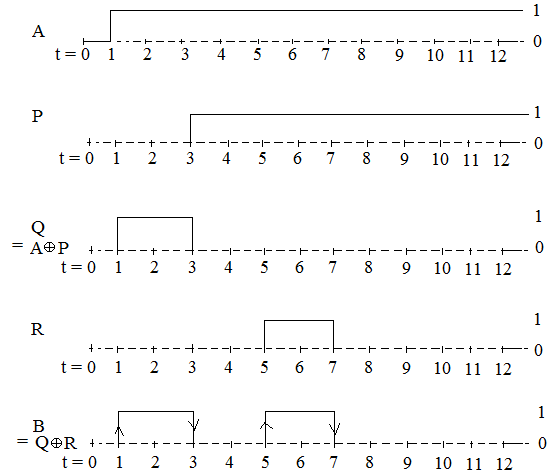
Note: Given sign is not an inverter but a buffer used for introducing delay.
∴ Output at ‘P’ and ‘R’ will be obtained at 2 ns and 4 ns respectively after the change in their inputs.
Hence, waveforms of ‘P’ and ‘R’ are shifted by 2 ns and 4 ns as compared to their inputs.
Also, note that ‘Q’ and ‘B’ are plotted using their corresponding input waveforms.
Finally, we can see that there are 4 changes in logic levels in the waveforms of ‘B’.
Ques 14: A Boolean function x′y′+xy+x′y is equivalent to
GATE 2004
(A) x’ + y’
(B) x + y
(C) x + y’
(D) x’ + y
Ans: (D) x’ + y
Solution: x’y’ + xy + x’y
=x’y’ + (x + x’) y
=x’y’ + y
=x’ + y
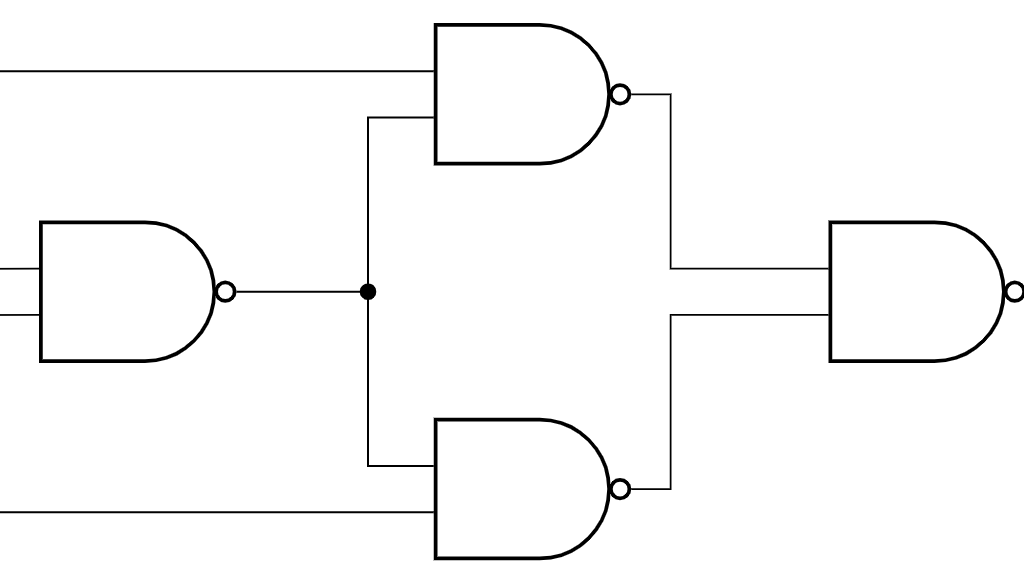
Ques 15: What is the minimum number of NAND gates required to implement a 2-input EXCLUSIVE-OR function without using any other logic gate?
GATE 2004
(A) 3
(B) 4
(C) 5
(D) 6
Ans: (B) 4
Solution:
| GATE | BY Using NAND | by using NOR |
| NOT | 1 | 1 |
| OR | 3 | 2 |
| AND | 2 | 3 |
| NAND | – | 4 |
| NOR | 4 | – |
| EX-OR | 4 | 5 |
| EX-NOR | 5 | 4 |