Program to generate Pascal’s Triangle in C

Pascal’s Triangle: It is a special triangle. All values outside the triangle are considered zero (0). The first row is 0 1 0 whereas only 1 acquire a space in pascal’s triangle, 0s are invisible. Second row is acquired by adding (0+1) and (1+0). The output is sandwiched between two zeroes. The process continues till the required level is achieved.

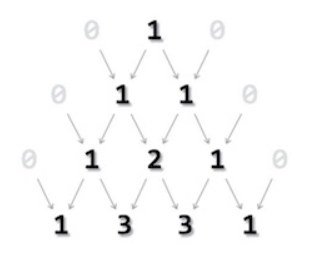
It can be derived using combinatories and factorials.

Algorithm:
1) Enter number of rows n
2) Repeat steps 3 to 6 for i= 0 to n-1 //for rows
3) for j=0 to n-i
print space
4) for j=0 to i
print ncr of i and j
5) print “\n” for next line

Program:

#include <stdio.h>
int factorial(int n)
{
    int f=1;
    for (int i=1; i<=n; i++)
        f = f * i;
    return f;
}
int findncr(int n, int r)
{
    return factorial(n) / (factorial(n - r) * factorial(r));
}

int main()
{
    int n, i, j;
    printf("**********************************************************\n");
    printf("**********************************************************\n");
    printf("**       WAP to generate a Pascal's Triangle            **\n");
    printf("**           Created by Sheetal Garg                    **\n");
    printf("**            Assistant Professor                       **\n");
    printf("**            Phone No:9467863365                       **\n");
    printf("**********************************************************\n");
    printf("**********************************************************\n");
    printf("Enter no of rows : ");
    scanf("%d" ,&n);
    printf("Pascal's Triangle is \n");
    for (i = 0; i <= n; i++)
    {
        for (j = 0; j <= n - i; j++)
            printf("  ");
        for (j = 0; j <= i; j++)
            printf(" %3d", findncr(i, j));
        printf("\n");
    }
    return 0;
}

Output:

**********************************************************
**********************************************************
**       WAP to generate a Pascal's Triangle            **
**           Created by Sheetal Garg                    **
**            Assistant Professor                       **
**            Phone No:9467863365                       **
**********************************************************
**********************************************************
Enter no of rows : 8
Pascal's Triangle is 
                     1
                   1   1
                 1   2   1
               1   3   3   1
             1   4   6   4   1
           1   5  10  10   5   1
         1   6  15  20  15   6   1
       1   7  21  35  35  21   7   1
     1   8  28  56  70  56  28   8   1